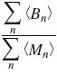Here’s another in my occasional series of posts detailing small results I’ve produced that aren’t worth being published anywhere but I’d quite like to jot down for my own or others’ reference.

Suppose you have a sequence of binary events. For definiteness, let’s say these are tosses of a weighted coin, where the probability of coming up heads is p (where p is not necessarily 0.5, because as I say, it’s a weighted coin).

What is the probability that, in a sequence of n coin tosses, at some point you will get two heads in a row?
I’ll denote that probability f(n,p).

The short answer is that for small p and low n, the answer is approximately, for n>4

f(n,p) = (n-1)p² – (n-2)p³ – 0.5(n-3)(n-4)p⁴ + (n-4)² p⁵ …

This is exact for n=5 and becomes less accurate as n increases thereafter.

I derived this by induction as follows.
It’s obvious that f(1,p) = 0 and f(2,p) = p².
And just by enumeration, I can say that f(3,p) = 2p² – p³.

For larger n, suppose the first toss is heads, with probability p. The probability that the 2nd toss is also heads is p again, and then we already have our two successive heads whatever else happens. If the 2nd toss is tails, probability (1-p), then there’s still a chance f(n-2,p) that there’s a sequence of 2 in the remaining (n-2) tosses.
And suppose the first toss is tails, probability (1-p). There’s still a chance f(n-1,p) that there’s a sequence of 2 heads in the remaining (n-1) tosses.
Thus we have the recursive relationship

f(n,p) = p² + (1-p) f(n-1,p) + p(1-p) f(n-2,p).

Thus one can derive, for example:
f(4,p) = 4*p² – 3*p³ – p⁴ + p⁵.

I worked out results up to f(12,p) and was able to spot the pattern given above, up to 5th order. Beyond that it gets beyond my abilities! However, here is a Matlab function to work out the exact solution iteratively. For example Prob2InSeq(100,0.03) = 0.082993772557983,Prob2InSeq(500,0.03) = 0.353773771895593. That is, you stand a 35% chance of getting two successive heads somewhere within 500 coin tosses, if the probability of heads is 3% on each coin toss.

1
2
3
4
5
6
7
8
9
10
11
12

function prob = Prob2InSeq(nn,p)
f(1) = 0;
f(2) = p^2;
f(3) = 2*p^2-p^3;
n=max(nn);
if n>3
    for m = 4:n
        % f(N,p) = p2 + (1-p) f(N-1,p) + p(1-p) f(N-2,p)
        f(m) = p^2 + (1-p)*f(m-1) + p*(1-p) * f(m-2);
    end
end
prob =  f(nn);

The graph below confirms my working. The blue curve is the exact value calculated by Prob2InSeq(n,p), with in this example p=0.03. The yellow scribbly line over it is the probability estimated from 100,000 simulated sequences of n coin tosses. The red curve that departs somewhat from them at high n is the 5th-order approximation given above.

Graph showing the probability of getting two successive heads in a row out of n tosses of a weighted coin, where the probability of heads on each individual toss is 0.03

I’ve just downloaded d’Aguilon’s 1613 “Six Books of Optics” from the Internet Archive ( Opticorum Libri Sex by Aguilonius). It’s such a joy to have this classic texts freely available now. The downside is that it tempts me to go down historical rabbit-holes rather than writing the lecture I should be writing on the evolution of stereopsis… but it’s fascinating so I can’t mind too much.

I’m struck by how ahead of his time this seventeenth-century Jesuit is. My mental summary of the history stereopsis had been something like: “People like Descartes and Kepler believed that vergence was a powerful distance cue, and Leonardo in his Treatise in Painting pointed out how interocular differences in occluded regions give a compelling sense of depth. However, the role of retinal disparity was not appreciated until Wheatstone’s 1838 presentation to the Royal Society. This showed for the first time that retinal disparity can give a depth percept with no change in vergence. More recently, vision scientists have pointed out how much more sensitive humans are to the relative disparity between objects or surfaces than to the absolute disparity of an isolated object.”.

I don’t know of an English translation, which probably wouldn’t be available freely on the Internet anyway. The Latin is rather beyond me (I did the A-level 30 years ago and that was classical rather than seventeenth-century scientific Latin). But as far as I can tell, Aguilonius argues that vergence is not a distance cue, and he lays out the importance of relative disparity quite clearly. I am surprised as I didn’t think those views were held so early.

Aguilonius’ Third Book of Optics is “de communium objectorum cognitione” , which I think might be translated as “on the perception of general objects”. As far as I can gather, he thinks there are 9 properties of objects: distantia( (distance), quantitas (size – “big or small, thick or thin, long or wide”), figura (shape – “straight or curved, convex or concave, acute or obtuse”), locus (3D location – “above/below, left./right, forward/back”), situs (stance – “sitting, standing, order, arrangement”), continuitas, discretio (these seem to be lumped together into what we might call numerosity), motus, quietus (motion and rest) . He says distance is the most important because the perception of the others depends on it (Distantiam praemittimus, ex cuius perceptione ceterorum cognitio dependet).

He then discusses cues to distance. He mentions known size (“who would deny that distance is inferred from the known magnitude of a thing, especially from that common notion, that a person judges those objects to be far away which appear small, when in reality they are large?”)

I don’t follow his “preliminary notes”, but I think he is emphasising the difficulty of what we would call metric depth: it is difficult to perceive not that an object is distant, but how far away it is.

The importance of binocular vision for depth perception

Proposition 1: “A single eye cannot define distance by itself”. He points out that all objects along a given line of sight project to the same point in the eye. He goes into the difficulty of depth perception with one eye covered, giving my favourite example of how hard it is to thread a needle. (“Hinc etiam filum per foramen acus transversum immittere, altero occluso oculo incerti negotii est”).

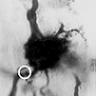
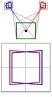
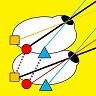
He mentions a game “which we learnt from boys, but judge worthy of a philosopher”: “The game was thus: one of the boys would hold a stick upright in his hand, while another would strive to touch it with his outstretched index finger while looking with only one eye; and whenever the stick was moved, he would almost always miss the goal.” (Lusus hic erat: puerorum alter bacillum erectum tenebat manu, hunc alter protenso in transversum indice tangere nitebatur uno tantum cernens oculo, ac quoties id moliebatur, toties paene a meta aberrabat) Aguilonius argues that they make these mistakes  because they can’t judge distance correctly. Rubens has illustrated this beautifully in the chapter heading :

Ono et al (Perception 42(1):45-49) argue that this illustration “is possibly depicting the cosmic observer performing Porta’s sighting test; having pointed to the stick, held by a putto, the observer closes the left eye to determine whether the finger is still aligned with the stick.” But I think given the above, it’s clear that Rubens is illustrating the game described, played by a philosopher since Aguilonius suggests it’s worthy of them.

Having made the case that you can’t judge distance mononocularly, Aguilonius immediately, in his second propsoition, gives us some exceptions, e.g. pointing out that due to the ground plane, height in the visual field enables us to infer distance with one eye:

Vergence

But it’s his third proposition that interests me most. As far as I can tell, he’s dissing the idea that vergence is a distance cue.

I’ll translate this as best I can:

“Proposition III. Theorem. Not correctly do some assert that distance can be known from the angles of the conjoined axes.

“There are those who want distance to be inferred from the magnitude of the angle made by the concurrent axes, so that the more distant objects are, the smaller the angle of the axes at the point where it intersects them; and the closer, the larger. Which they try to show in this way. Let there be two eyes A and B, and let CD be a general line. It doesn’t matter whether CD is orthogonal to the line connecting the centres of sight [AB], or oblique. Now let there be a visible object on the general line, now at E, now at D. With optic axes being drawn from E and D to each appearance, DA and DB and ditto EA and EB, the angle AEB will be greater than the angle ABD by the 21st theorem of the first book of Euclid: if indeed E falls within the triangle ADB.
Wherefore E will be shown to be closer, since it appears with a larger angle, and D further, since lesser. This demonstration seems solid to them: but really it is confounded most strongly by two arguments. The first is this: Sight does not perceive the magnitude of the angle which the axes make in their concourse: for it is outside the eye; nor is it imbued by any visible qualities by which it could be seen. For things which are outside the eye cannot be known except by their sensed properties; but things in the eye can be felt by the very same sense, such as the movement of the eyes, and their position, the operation of vision itself, and other things of this kind: not therefore by the work of that very angle can vision know the distance of things.”

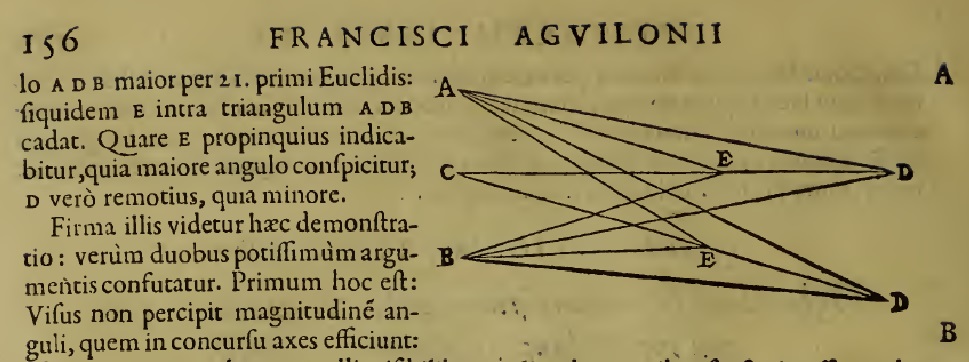
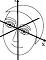
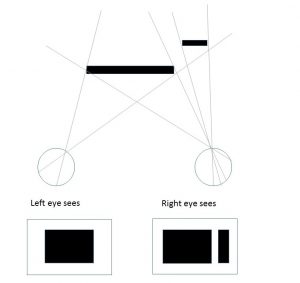
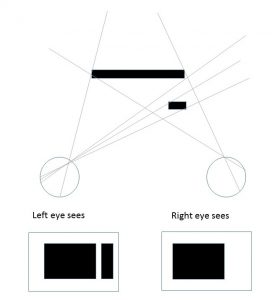
His other killer argument is that points on the horopter have the same vergence angle but are at different distances, as shown here:

NB the wikipedia entry for horopter states “The term horopter was introduced by Franciscus Aguilonius in the second of his six books in optics in 1613.[5] In 1818, Gerhard Vieth argued from Euclidean geometry that the horopter must be a circle passing through the fixation-point and the nodal point of the two eyes.” But from the above diagram it seems pretty clear Aguilonius had already arrived at Vieth’s conclusion 200 years earlier.

I may be misunderstanding but I read the above as a pretty clear statement that vergence is not available from purely ocular information [he doesn’t know about modern photogrammetry and is considering a 2D system] and he seems to be rejecting the idea that extra-ocular information would be used to interpret visual information. This goes counter to what I thought I knew: that vergence was considered a strong distance cue at this time.

Relative disparity

Proposition IV is “Distance is recognised from the length of the optic axes”. This does not sound very promising but I think it’s actually a statement about relative disparity, which struck me as remarkably ahead of its time. Aguilonius confused me by talking about “the length of the optic axes” – how could you obtain that from visual information? But he’s pointing out you can infer that from the other eye. He refers us back to Proposition XXIV of the Second Book: “The length of one optic axis is perceived by the other eye from the size of the angle made by its own axes with the interocular axis”.

“Let there be two centres of projection, A and B, and let the axis of eye A be the line AC, whose magnitude I say can be recognised from the viewpoint of B by the size of the angle ABC made by its own optic axis BC and the line AB connecting the centres of projection”.

Now as an argument for metric depth, this is a bit flawed. Aguilonius is trying to get metric depth from absolute retinal disparity, but he hasn’t appreciated that the criticism he made in Proposition II of Book III also applies here: the position of the interocular axis AB is “outside the eye” and cannot be deduced from the visual information he is discussing. He later argues (correctly in my view) that the angle ADB in this diagram isn’t directly available from retinal information, but he assumes that the angle DBA is – and I disagree.

But I think in Book III, Proposition IV, he uses this line of argument much more convincingly.

“It sometimes occurs that a visible object on the same axis BD now becomes closer, as in C, now more distant, as in D. When this happens, in the same way as the eye B sees both axes AC and AD as equal, since each subtends the same angle ABC; in the same way eye B perceives points C and D as equally distant, or to put it better, it does not discern their unequal distances, since it judges equal to be equally distant: for as was shown in Proposition I of this book, eye B alone cannot perceive the distance of objects on a straight line drawn from the eye. But eye A, bringing its own action also to bear in common, resolves the question. For eye A, grasping that line BC is shorter than BD, defines the object C as being nearer to B than point D. Thus, from the lengths of the optic axes, two eyes together, by their joint power, lead to the perception of distance, which neither could achieve by its solitary action.”

Notice that here he doesn’t make a case for metric depth: he’s just arguing that binocular vision enables us to see that C is closer than D. I think this is a fairly clear statement about depth perception from relative disparity, explicitly not dependent on vergence.

Perhaps I’m being too generous since he seems to be considering the relative disparity between the same object at different times (“nunc propinquius fit, nunc remotius“) rather than the relative disparity between two simultaneously visible objects. Nevertheless I was surprised to see this in 1613, 250 years before Wheatstone’s creation of stereograms. What do other vision scientists think?