Here’s another in my occasional series of posts detailing small results I’ve produced that aren’t worth being published anywhere but I’d quite like to jot down for my own or others’ reference.

Suppose you have a sequence of binary events. For definiteness, let’s say these are tosses of a weighted coin, where the probability of coming up heads is p (where p is not necessarily 0.5, because as I say, it’s a weighted coin).

What is the probability that, in a sequence of n coin tosses, at some point you will get two heads in a row?
I’ll denote that probability f(n,p).

The short answer is that for small p and low n, the answer is approximately, for n>4

f(n,p) = (n-1)p² – (n-2)p³ – 0.5(n-3)(n-4)p⁴ + (n-4)² p⁵ …

This is exact for n=5 and becomes less accurate as n increases thereafter.

I derived this by induction as follows.
It’s obvious that f(1,p) = 0 and f(2,p) = p².
And just by enumeration, I can say that f(3,p) = 2p² – p³.

For larger n, suppose the first toss is heads, with probability p. The probability that the 2nd toss is also heads is p again, and then we already have our two successive heads whatever else happens. If the 2nd toss is tails, probability (1-p), then there’s still a chance f(n-2,p) that there’s a sequence of 2 in the remaining (n-2) tosses.
And suppose the first toss is tails, probability (1-p). There’s still a chance f(n-1,p) that there’s a sequence of 2 heads in the remaining (n-1) tosses.
Thus we have the recursive relationship

f(n,p) = p² + (1-p) f(n-1,p) + p(1-p) f(n-2,p).

Thus one can derive, for example:
f(4,p) = 4*p² – 3*p³ – p⁴ + p⁵.

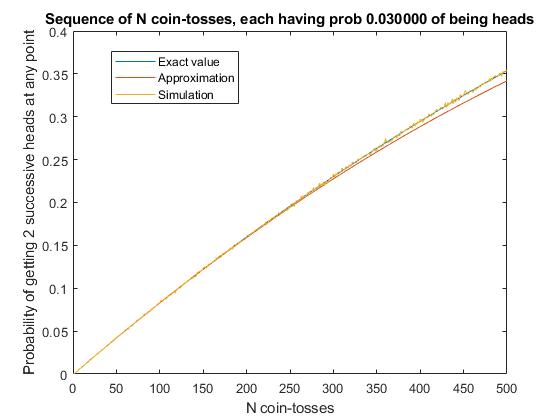
I worked out results up to f(12,p) and was able to spot the pattern given above, up to 5th order. Beyond that it gets beyond my abilities! However, here is a Matlab function to work out the exact solution iteratively. For example Prob2InSeq(100,0.03) = 0.082993772557983,Prob2InSeq(500,0.03) = 0.353773771895593. That is, you stand a 35% chance of getting two successive heads somewhere within 500 coin tosses, if the probability of heads is 3% on each coin toss.

1
2
3
4
5
6
7
8
9
10
11
12

function prob = Prob2InSeq(nn,p)
f(1) = 0;
f(2) = p^2;
f(3) = 2*p^2-p^3;
n=max(nn);
if n>3
    for m = 4:n
        % f(N,p) = p2 + (1-p) f(N-1,p) + p(1-p) f(N-2,p)
        f(m) = p^2 + (1-p)*f(m-1) + p*(1-p) * f(m-2);
    end
end
prob =  f(nn);

The graph below confirms my working. The blue curve is the exact value calculated by Prob2InSeq(n,p), with in this example p=0.03. The yellow scribbly line over it is the probability estimated from 100,000 simulated sequences of n coin tosses. The red curve that departs somewhat from them at high n is the 5th-order approximation given above.

Graph showing the probability of getting two successive heads in a row out of n tosses of a weighted coin, where the probability of heads on each individual toss is 0.03