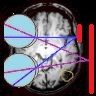
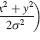There are many ways of thinking about epipolar geometry. Here’s one. This page contains a couple of videos I created showing how the epipolar lines rotate on the retina as the eyes move.
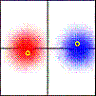
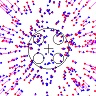
The two eyes are viewed from behind. The coordinates show lines of longitude for both elevation and azimuth on the retina.
The red dots show the 13 points on the left retina for which I calculated possible matches in the right — the epipolar lines shown in blue. This works as follows. For each red dot, I project a ray back out into space. If you only had the left eye, all you would know about the object that generated this red dot is that it must lie somewhere along this ray. I then project each point on the ray into the right eye. The set of these points forms the blue line in the right eye. This is the line of possible “matches” for the red dot. This epipolar line runs from near the “east pole”, for objects just in front of the left eye, to just beyond the red dot (reproduced on the right retina for comparison), for objects at infinite distance. Retinal locations to the right of the red dot have crossed disparity; those to its left have uncrossed disparity.
In primary position, when both eyes are loking straight ahead to infinity, all points on the epipolar line have the same elevation as the original red dot, so there is no vertical disparity. However, as the eyes move, the epipolar lines swing away from the black lines of constant retinal elevation. In general, the vertical disparity increases with horizontal disparity — ie the difference in retinal azimuth between the original red dot and its match on the blue line.
Details
The eyes are 6.5cm apart, and the fixation distance varies between 27cm and 120cm. The eyes move according to a binocular extension of Listing’s law, as described in Somani et al. 1998 (Vis Res 38:911, eq 11). This means that for non-zero elevations, the eyes have small amounts of Helmholtz torsion. The coordinate systems on the two retinas are aligned so that with both eyes pointing straight ahead to infinity, points at infinity would project to the same coordinates in both retinae. Lines of longitude are plotted every 15 degrees between +/-90 degrees.
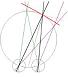
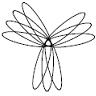
The video below shows how the fixation point moves in space during the above movies. I wanted to get a range of combinations of elevation and azimuth,
so I just made the fixation point describe a random Lissajous figure.
You can download the videos here: