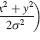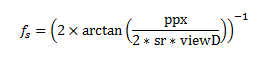I was just looking for a good explanation of this online to point a lab member towards, and I couldn’t find anything suitable, so I thought I’d write something myself. (Since then, this https://en.wikipedia.org/wiki/Fraction_of_variance_unexplained seems pretty good.

The idea is you have a set of experimental data {Yi} (i=1 to N). These might be responses collected in N different conditions, for example.
The mean is

M = sum{Yi} / N

and the variance about this mean is the total variance

TV = var(Yi) = sum{ (Yi-M)^2 } / N

Now suppose you have some model or fit which predicts values Fi. The residuals between the fit and the data are Ri=(Yi-Fi). The mean of the squared residuals is

RV = sum { (Yi - Fi )^2 } / N

(this is identical to the variance of the residuals if Fi and Yi have the same mean, as they do in linear regression)
The fraction of UNexplained variance is RV/TV, so the fraction of explained variance is 1-RV/TV.

In a perfect world, Fi would be equal to Yi for all i, and therefore these residuals would all be zero. RV=0 and thus all of the variance is explained. The other end of the spectrum is where all the fit values are the same, just equal to the mean of the data: Fi=M. Then we can see from the equations above that RV=TV and none of the variance is explained.

The percentage of variance which is explained is

PV = 100(1-RV/TV).


The Warping Effect

In our mantis contrast sensitivity paper (http://tinyurl.com/mantiscsf) we used the following formula to calculate the spatial frequency of grating stimuli in cycles per degree (cpd):

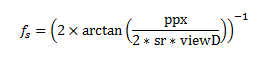
Where ppx is the grating period in pixels, sr is the screen resolution in px/cm and viewD is the viewing distance in cm.

This equation assumes a linear correspondence between screen pixels and the visual angle subtended by these pixels (in degrees). The conversion ratio is effectively the average over one grating period; for example a spatial period of 100px corresponds to 20.25 degs making the effective conversion ratio 4.94 px/deg.

When viewD is sufficiently large (which is typical for human experiments) the assumption of a linear correspondence between screen pixels and angle subtended holds (i.e. differences are negligible). However, for small viewD there could be considerable differences as gratings subtend smaller angles the further they are from the centre and thus the stimulus appears to be “squeezed” near the screen ends.

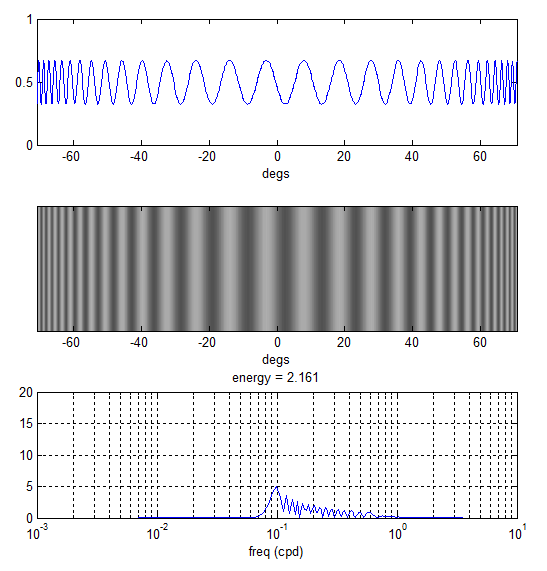
The plots below demonstrate this effect. The top two plots show a horizontal sinusoidal grating of period 5 px (sr = 40 px/cm) as perceived by an observer 7cm away from the monitor. Instead of a constant frequency in cpd there is actually a range of frequencies going from low (at the screen centre) to high (at both ends). The bottom plot is a frequency spectrum showing how broadband this actually is. Using the equation above fs = 0.978 cpd for this stimulus while the actual spectrum goes from 0.08 all the way up 0.6 cpd.

How to correct for this

One way to correct for this is to incrementally increase the grating period as we move away from the screen centre. For an observer standing sufficiently away from the monitor such a stimulus would appear squeezed at the centre and stretched at the sides. At the right viewing distance, however, all gratings will subtend the same visual angle.

This can be done in multiple ways in Matlab. I’ve found the following particularly intuitive and easy to implement:

1. Calculate the visual degree corresponding to each px on the screen given a viewing distance and a screen resolution (the function px2deg does this for you)
2. Use the obtained degrees array to calculate grating/stimuli luminance level

For example, to render a sinusoidal grating of frequency 0.1 cpd on a monitor that is 1920px wide I do:

scrWidthPx = 1920; % px
screenReso = 40; % px/cm
viewD = 7; % cm
freq = 0.1; % cpd
degs = px2deg(scrWidthPx, screenReso, viewD);
y = cos(2*pi*degs*freq);

The array y now contains 1920 luminance levels which, when rendered horizontally across the 1920 screen pixels, would simulate a grating of 0.1 cpd at the specified viewing distance. The plots below demonstrate how this is perceived by the observer.

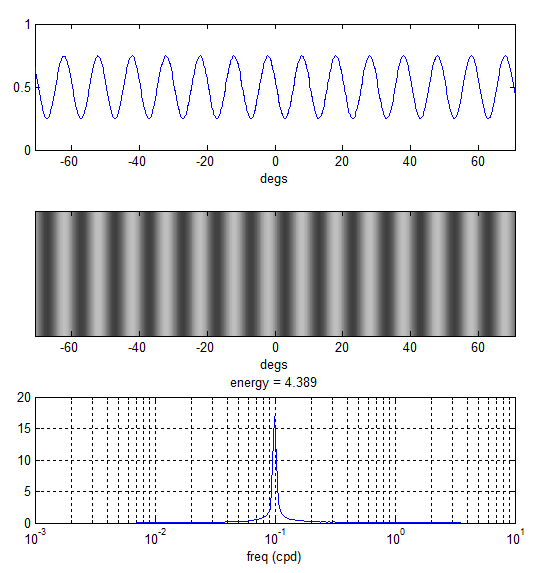
The rendered stimulus is now narrow-band as intended.

 Precautions

The correction above assumes a certain viewing distance and that the observer is positioned laterally in front of the screen centre. If the observer position changes then the perceived stimulus will have a different spectrum and so it is important to ensure that subjects (in our experiments, mantids) are placed at the correct viewing distance both away from the screen and laterally to minimize any errors.

How does this affect our CSF Data

The “warping effect” that we described above must be taken into consideration when interpreting the data we published in the mantis CSF paper. Each spatial frequency we rendered was actually perceived by the mantis as a broadband signal and so the actual mantis CSF is likely more narrow-band compared to what we reported.