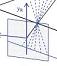
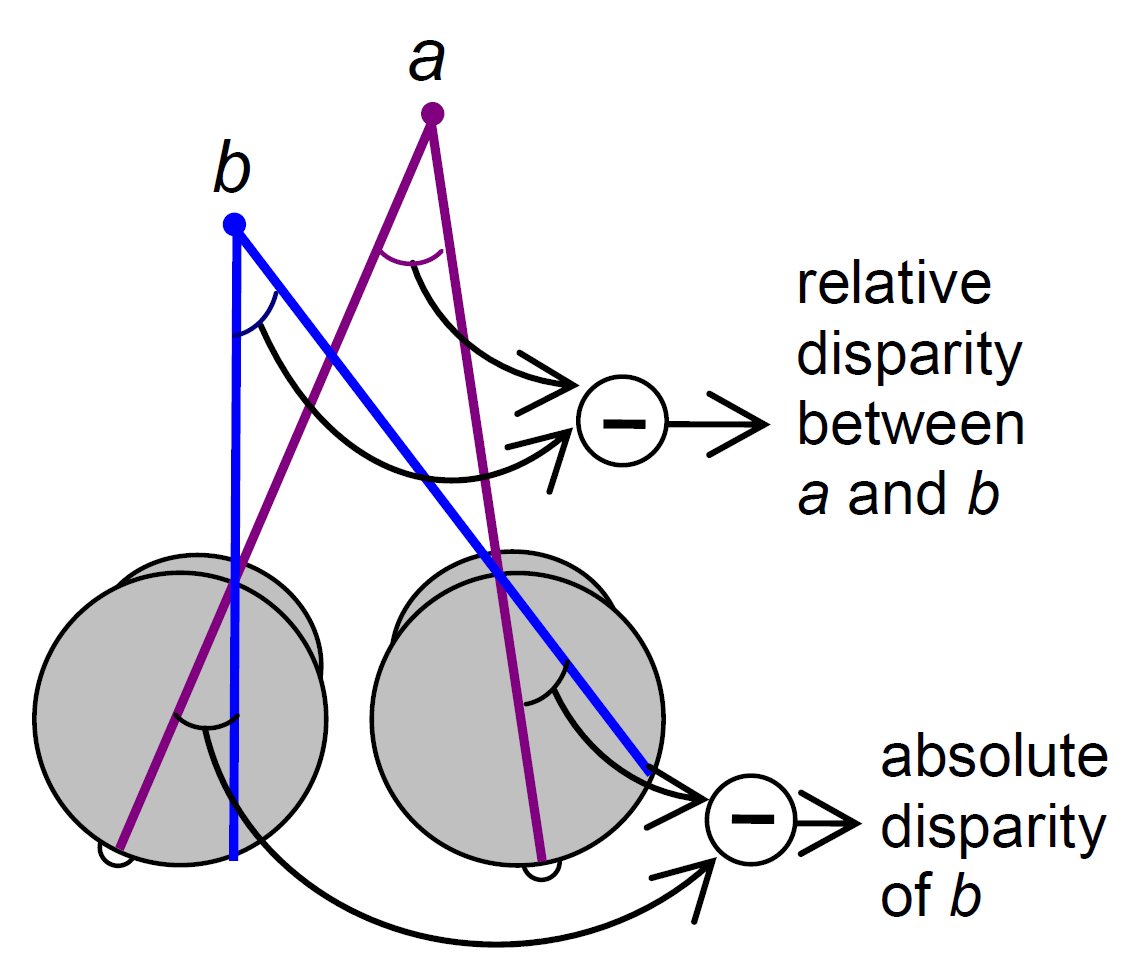
I thought it might be useful to point out a property of relative disparity. One way is as Andrew Parker does in his 2007 review: Relative disparity = (alpha-beta) in the diagram below.

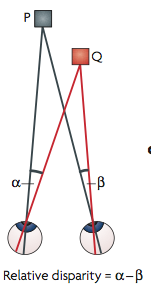In the special case where P is the fixation point, then alpha and beta are the retinal coordinates of the left and right images of Q, and the difference (alpha-beta) is the absolute disparity of the point Q.

If P is not the fixation point, (alpha-beta) is not the absolute disparity of Q, but it is still the relative disparity between the points P and Q.

In one of our papers, we used a slightly different definition which is probably less intuitive but is a handy way of looking at it:

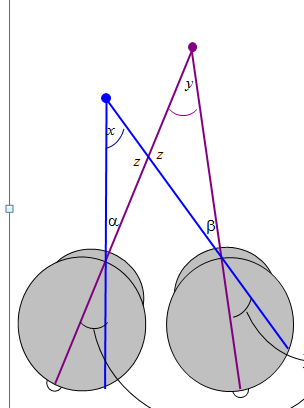
As the following diagram shows, these two definitions are actually the same:

Parker (2007) says relative disparity = (alpha-beta).

Read et al (2010) says relative disparity = (y-x).

But look at the triangles. 180^o = x + z + alpha = y + z + beta. Thus, (alpha-beta) =(y-x) and the two definitions are identical.